By far the most frequent question teachers ask me is “Where can I find good problems?”
They’re tired of spending hours and hours online searching for good problems that fit their content standards. Inevitably getting pulled into time-sucking rabbit holes on Teachers Pay Teachers, Pinterest, and Google.
The reality is there is just so much bad math to sort through online to find the hidden gems.
Why not just use your curriculum resources and textbook (assuming your school hasn’t left everything up to you.)?
Textbook publishers hire “experts” and spend thousands of man-hours creating materials and many teachers still feel like those resources aren’t good enough.
As someone who has taken on the challenge of trying to write engaging problems for a textbook, I can tell you it’s really hard.
Teaching math is about creating engaging and meaningful experiences.
That means being thoughtful about how you launch a task, knowing what information to reveal and what to keep secret, what questions to ask, what manipulatives or other tools are students will need, anticipating and addressing student questions, posing extension questions, and so on.
The moment you put a task in a book, you lose almost all of that!
Let’s see if we can quickly make a “bad” problem into a great math learning experience.
Here’s a 1st grade problem from a popular elementary textbook publisher.

What’s wrong with it?
First, this is a LOT of words for a first grader to parse! Second, I don’t imagine many first graders who read it would find it interesting.
Let’s Try to Craft a Better Experience
We need to find a way to eliminate the words and spark some curiosity.
One strategy you can try is Make it Visual, then apply Notice and Wonder at the launch.
Here was my first attempt (note I changed up the doors and floors a bit):
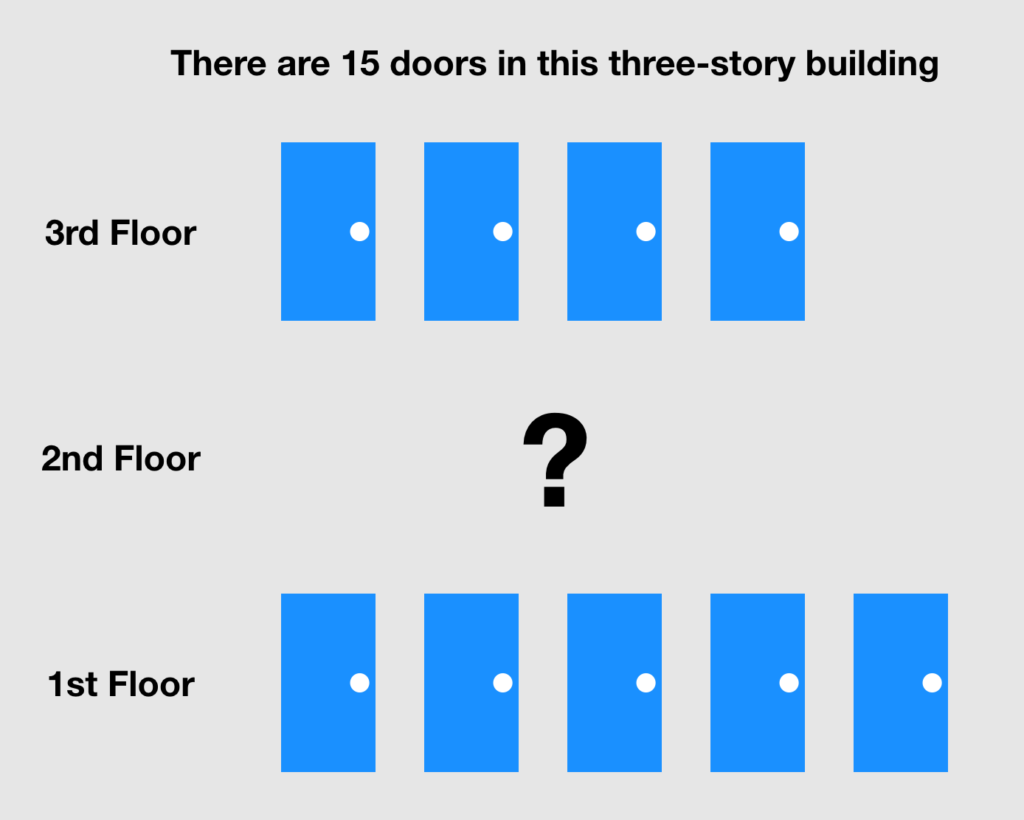
I could use this to ask students what they notice and wonder. I think that’s already a great start. We’ve eliminated the reading requirement, given students time to make sense of the scenario, and allowed them to pose their own questions. Engagement is bound to go up.
I wanted to see if I could remove the one sentence completely, so I added numbers to the doors.

I like this better because there is a little more for them to make sense of just by being observant. I think we have a strong launch. Note: This is a matter of learning goals and taste. You might choose the other option for good reasons.
Did we also get any deeper mathematics? Is it open to more than one strategy? Are there places students could go wrong?
Let’s start by anticipating how students might solve it (Step 1 of the Five Practices).
1: Count all the doors picture, then count on to 15
2: Subtract 12 – 5
3: Count on from 5 to 12
4: Add 5 + 4, then subtract from 15
5: …
Looks like we have a mix of concrete and abstract solutions. A good mix from which to generate a connected math discussion (Step 5 of the Five Practices).
Aside: Thanks to James Tanton for #2 which I didn’t think about on my own. That’s the power of work with your teacher team. This strategy generates a wrong answer for a subtle reason which could lead to a great conversation in a first grade classroom!
We’ve created a an experience that sparks some curiosity, creates a richer task, and leads to meaningful discourse about mathematics. That’s a win-win-win.
My goal with this is provide examples from which you can learn and apply in a short amount of planning time while avoiding an internet full of rabbit holes!
Today’s problem crafting technique was Make it Visual
With practice, you can start doing this on your own in a reasonable amount of time. Much quicker that a trip into the black hole that is the internet!